과거 시계열 데이터로 주식 수익률을 분석한 표(table)를 보면 산술평균 수익률(Average Return)과 기하평균 수익률(Compound Return)을 보게 됩니다. 둘의 차이는 무엇일가요?
아래의 사례를 보겠습니다. 1,000달러 투자하여 5년간 10% 수익률을 기록했고 투자금은 원금과 이자 수익을 포함하여 1,610.51 달러가 되어 있습니다. 여기서 수익률 10%는 기하평균 수익률을 의미합니다.
- Year 1: $1,000 x 10% = $1,100
- Year 2: $1,100 x 10% = $1,210
- Year 3: $1,210 x 10% = $1,331
- Year 4: $1,331 x 10% = $1,464.10
- Year 5: $1,464 x 10% = $1,610.51
산술평균으로 계산해볼까요? 단순하게 산술평균으로 계산 하면 수익률 10%일 경우, 1,000달러의 5년 후에 1,500달러이어야 합니다. 왜냐하면 500달러 수익을 5년 기간으로 나누면 매 년 100달러 수익이 발생했고 이는 투자 원금 1,000달러의 10%이기 때문입니다. 만약에 투자금 1,000달러가 5년 후 1,610.51달러로 증가했다면, 산술평균 수익률로 계산할 시, [(1,610.51-1,000)/1,000] / 5 = 12.2%가 되어야 합니다.
아래는 제임스 오셔너니 자산운용사에 작성한 "저PER 십분위수 수익률 분석" 표를 사례로 가져왔습니다. 연 수익률을 계산하는데 산술평균(Average Retrun)과 기하평균(Compound Return)을 함께 사용한 것을 볼 수 있습니다.


기하평균 수익률은 산술평균 수익률에 "투자 기간"을 포함한 개념입니다. 즉, 복리(compund) 개념을 포함하고 있습니다. 일정 기간 동안 원본 자금의 이익 혹은 손실을 누적적(cultimulative)으로 설명합니다. 산술평균 수익률은 일반적으로 연간 단위, 백분율로 표시됩니다. 즉, 산술평균 수익률은 투자 원금의 기간이 지남에 따른 누적적 복리 효과를 연간 백분율로 보입니다.
연간 단위로 표현하는 복리 수익률(compound return)을 CAGR(Compund Anuual Growth Rate)라고 합니다.
산술평균 수익률은 직관적으로 이해되는 반면, 기하평균 수익률은 그렇지 않습니다. 산술평균과 기하평균의 계산 방식을 이해할 필요가 있습니다. 아래 수식으로 살펴볼까요? 수학적 기호와 영어가 있어서 복잡해 보이지만 인내심을 갖고 보면 어렵지 않습니다 ^^
산술평균(Arithmetric Mean)은 모든 값을 더한 후 그 개수로 나누어 계산합니다. 반면에, 기하평균(Geometric Mean)은 모든 값을 곱한 후 그 개수로 거듭제곱하여 계산합니다.
산술평균(Arithmetric Mean)

기하평균(Geometric Mean)

지적인 학습자를 위한 심화학습
지적인 학습자라면, 조금 더 나아가 산술(Arithmetric)과 기하(Geometric)의 차이를 살펴볼 필요가 있습니다.
산술은 산수(算數), 즉 숫자를 셈하다라는 의미를 갖고 있습니다. 더하기, 빼기, 곱하기, 나누기와 같이 숫자를 셈합니다.
반면에 기하(幾何)는 꼴, 크기, 위치 즉, 도형에 관한 것입니다.
기하학적으로 볼 때, 2차원에서 넓이를 그대로 유지하면서 직사격형(rectangle)을 정사각형(square)으로 바꿀 때 기하평균이 사용됩니다. 가로, 세로 a, b인 직사각형의 넓이와 같은 정사각형의 한 변의 길이 2√ab가 기하평균 입니다. 3차원에서는 부피의 변화없이 직육면체(cuboid)를 정육면체(cube)로 바꿀 때 기하평균이 사용됩니다. 가로, 세로, 높이가 a, b, c인 직육면체와 부피가 같은 정육면체의 한 변의 길이 3√abc가 기하평균 입니다.
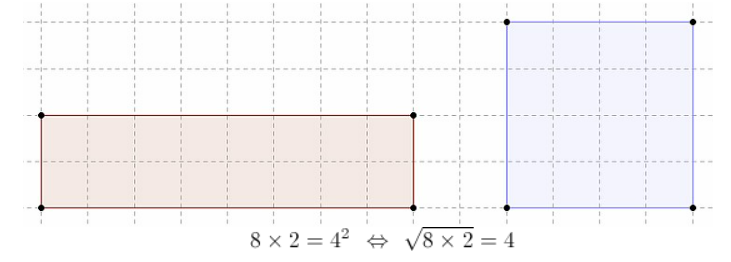
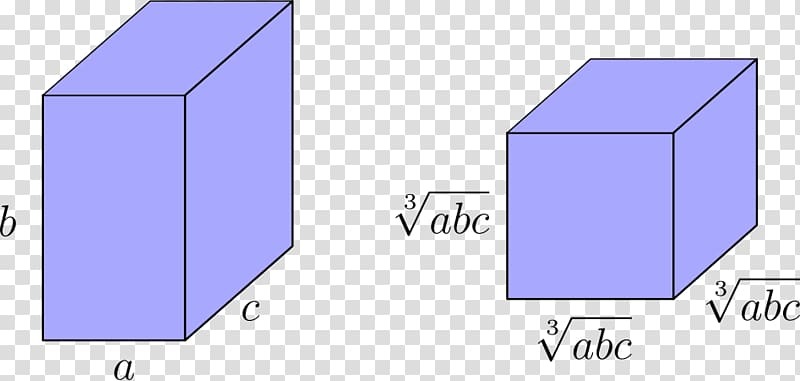
글의 처음 예시를 다시 살펴보겠습니다. 1,000달러를 기하평균 10% 수익률로 5년간 투자하면 투자원금은 1,000달러에서 1,610.51 달러가 되어 있었죠. 이를 산술평균 수익률로 표시하면 12.2% 수익률이 됩다. 기하평균 수익률은 기하의 개념이 적용되어 투자 기간에 맞춰 연간 동일하게 환산된 수익률인 개념인 반면에, 산술평균 수익률은 산술의 개념으로 단순하게 처음과 끝의 차이를 나눈 수익률입니다. 마치 직사각형을 정사각형으로 직육면체를 정육면체로 "차원"에 따라 변환한 것처럼, 산술평균 수익률을 기하평균 수익률로 "투자 기간"에 맞게 변환한 것입니다.
참고 자료
월가의 퀀트 투자 바이블
https://www.investopedia.com/ask/answers/06/geometricmean.asp
Arithmetic Mean vs. Geometric Mean: What's the Difference?
Investors usually consider the geometric mean a more accurate measure of portfolio performance than the arithmetic mean because it accounts for compounding. Learn more.
www.investopedia.com
https://www.investopedia.com/terms/c/compoundreturn.asp
Compound Return: Definition, How It Works and Example Calculation
The compound return is the rate of return that represents the cumulative effect that a series of gains or losses has on an amount of capital over time.
www.investopedia.com
blog.naver.com/alwaysneoi/100156668769
[산술평균과 기하평균의 관계] 산술평균이 기하평균보다 항상 크거나 같다.
산술평균(Arithmetic Mean) 각 양수들을 모두 더하여 그 개수로 나눈 값이다. 우리가 보통 말하는 평균이...
blog.naver.com
'금융투자' 카테고리의 다른 글
| [싱가포르의 기적] 싱가포르 부동산 산업의 발전 (1) | 2023.09.22 |
|---|---|
| [책 리뷰] 존 리, 새로운 10년의 시작 | 존리 | 김영사 (0) | 2023.09.19 |
| [책 리뷰] 새로운 금융이 온다 | 헨리 아슬라니언 | 차밍시티 (2) | 2023.09.16 |
| [책 리뷰] 리츠 투자 무작정 따라하기 | 김선희 | 길벗 (0) | 2023.09.16 |
| [책 리뷰] 벤저민 그레이엄 자서전 | 벤저민 그레이엄 | 차이정원 (2) | 2023.09.13 |



